지난 글에서 말했던 대로 이번에는 연속확률분포에서의 ABC에 대해 이야기하겠습니다. 가장 큰 차이는 acceptance의 기준을 바꾸어야 한다는 것입니다. 이항분포의 경우에는 원 자료와 완전히 같은 자료를 생성하는 모수치만 accept하는 게 가능했지만, 연속확률분포에서는 그렇게 할 수가 없습니다. 이유는 말 안 해도 잘 아시죠? 사실 이항분포에서도 시행횟수(n)가 충분히 크면 원 자료와 완전히 같은 자료가 생성되기 무척 힘들고, 이로 인해 대부분의 proposal들이 기각돼 버려서 샘플링에 시간이 많이 걸린다는 단점이 있습니다. 그래서 이 글에서 이야기할 방법을 사용하는 게 도움이 됩니다.
이제는 accept/reject를 판단하는 기준을 좀 바꿔서, 약간의 ‘차이’는 허용하겠습니다. 수정된 ABC 알고리즘의 한 ‘바퀴’는 다음과 같습니다:
- 사전분포에서 모수치 제안
- 제안된 모수치를 이용해 자료 생성
- 생성된 자료와 원 자료 사이의 ‘거리’를 계산
- 계산된 거리가 어떤 문턱값 threshold보다 작으면 제안된 모수치 수락, 아니면 1로 돌아감.
이를 모분산을 아는 정규분포의 모평균 추정 문제에 적용하면 다음과 같은 알고리즘이 될 것입니다:
- 사전분포에서 모평균 제안
- 제안된 모평균과 모분산을 이용하여 자료 생성
- 생성된 자료와 원 자료 사이의 ‘거리’를 계산
- 계산된 거리가 어떤 문턱값 threshold보다 작으면 제안된 모수치 수락, 아니면 1로 돌아감.
이제 여기서 말한 ‘거리’를 정의해야 하는데, 앞선 글에서 말했던 대로 되도록 충분통계량을 활용하는 게 좋습니다. 모평균에 대한 충분통계량은 물론 표본평균이기 때문에, 이것을 이용하여 거리를 정의하겠습니다. 이를테면 원 자료의 표본평균과 생성된 자료의 표본평균의 차이 절댓값을 거리로 정의하면 됩니다. (물론 그 제곱을 활용한다든지 할 수도 있습니다.)
이제 이것을 구현해 보겠습니다. 자료의 크기는 \(=100\)이고, \(N(100, 15^2)\)에서 온다고 가정하겠습니다. 사전분포는 \(N(90, 30^2)\)을 사용하겠습니다:
# R
set.seed(111)
# settings
n <- 30
mu_true <- 100
sd_true <- 15
prior_mean <- 90
prior_sd <- 30
# Python
from numpy.random import normal
from numpy import mean, std
# settings
n = 30
mu_true = 100.0
sd_true = 15.0
prior_mean = 90.0
prior_sd = 30.0
이제 자료를 생성해 보겠습니다:
# R
# generate data
data <- rnorm(n, mu_true, sd_true)
mean_sample <- mean(data)
mean_sample
[1] 97.1779
# Python
# generate data
data = normal(mu_true, sd_true, n)
mean_sample = mean(data)
print(mean_sample)
이제 사후분포를 구해봅시다. 참고로 자료생성 모형도 정규분포, 모평균의 사전분포도 정규분포인 경우 모평균에 대한 사후분포도 정규분포가 됩니다. 그러니까 정규분포는 자기 자신에 대한 conjugate prior인 셈이죠? 그 사후분포의 평균과 분산은 다음과 같이 구할 수 있습니다 (구체적인 공식은 [1]을 참조하세요):
# R
# Theoretical posterior quantities
post_prec <- 1/prior_sd^2 + n/sd_true^2
post_sd <- sqrt(1/post_prec)
post_mean <- (prior_mean/prior_sd^2 + mean_sample/(sd_true^2/n))/(1/prior_sd^2 + n/sd_true^2)
post_mean
[1] 97.11857
post_sd
[1] 2.727273
# Python
# Theoretical posterior quantities
post_prec = 1/prior_sd**2 + n/sd_true**2
post_sd = (1/post_prec)**(0.5)
post_mean = (prior_mean/prior_sd**2 + mean_sample/(sd_true**2/n))/post_prec
print(post_mean)
print(post_sd)
이제 ABC sampling을 통해 이 값들을 재현할 수 있나 보겠습니다. 일단 ABC rejection sampler는 다음과 같이 작성할 수 있습니다:
# R
# ABC rejection sampler
sampler <- function(n, sd_true, prior_mean, prior_sd, mean_sample, eps){
dist <- eps + 1
while(dist > eps){
mu_proposal <- rnorm(1, prior_mean, prior_sd)
mean_sim <- mean(rnorm(n, mu_proposal, sd_true))
dist <- abs(mean_sim - mean_sample)
}
mu_proposal
}
# Python
# ABC rejection sampler
def sampler(n, sd_true, prior_mean, prior_sd, mean_sample, eps):
dist = eps + 1
while dist > eps:
mu_proposal = normal(prior_mean, prior_sd, 1)
mean_sim = mean(normal(mu_proposal, sd_true, n))
dist = abs(mean_sim - mean_sample)
return(mu_proposal)
실제로 샘플링을 해 보면 다음과 같습니다. Accpet 여부를 결정하는 문턱값(eps)으로는 0.5를 사용하겠습니다. 여기서 eps가 작을수록 posterior는 정확하게 추정되겠지만 계산 시간이 훨씬 더 많이 걸릴 수 있으니, 적절히 조절돼야 합니다:
# R
# ABC sampling
eps <- 0.5 # threshold for acceptance
n_mcmc <- 10000
post <- vector(length=n_mcmc)
for(i in 1:n_mcmc){
post[i] <- sampler(n, sd_true, prior_mean, prior_sd, mean_sample, eps)
}
# Python
# ABC sampling
eps = 0.5 # threshold for acceptance
n_mcmc = 10000
post = []
for i in range(n_mcmc):
post.extend(sampler(n, sd_true, prior_mean, prior_sd, mean_sample, eps))
이제 사후분포의 평균과 표준편차를 계산해 보면 다음과 같습니다:
# R
# Posterior quantities computed from the sample
mean(post)
[1] 97.11091
sd(post)
[1] 2.757013
# Python
# Posterior quantities computed from the sample
print(mean(post))
print(std(post))
앞에서 구한 값들과 큰 차이가 없음을 확인할 수 있습니다. Posterior sample에 이론적 사후분포를 함께 그린 것은 아래 그림에서 확인할 수 있습니다.
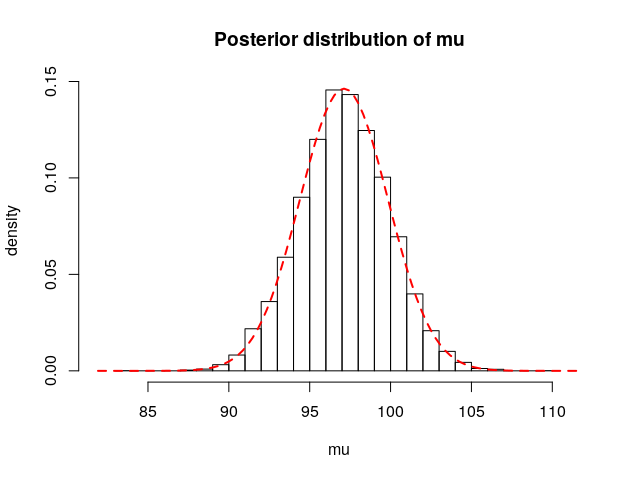
지금까지 연속확률분포에서 ABC를 구현하는 예시를 보았습니다. 생각보다 간단하(?)죠? 사실 실제 적용에서는 rejection sampling은 잘 사용하지 않는데, 그보다는 효율성이 더 나은 ABC MCMC라는 것을 많이 사용합니다. 이에 대한 구체적인 설명은 생략합니다. 자세한 것은 첫 글에 언급된 Turner & Van Zandt (2012) 을 참조하시기 바랍니다.