베이지안 통계에 대해 가해지는 비판들 중 가장 흔한 것은 역시 분석 결과가 사전분포 prior distribution 의 영향을 크게 받는다는 것입니다. 사전분포는 분석가의 주관적 믿음 (사실 저는 이 표현을 썩 좋아하지는 않습니다만) 을 반영하는 것이기 때문에, 서로 다른 분석가가 서로 다른 사전분포를 썼을 때 서로 다른 분석 결과에 도달하게 된다는 것은 당연합니다. 그래서 이 글에서는 앞에서 예시로 든 베이지안 메타분석의 예를 들어, 사전분포가 결과에 어떤 영향을 미치는지 한 번 알아보겠습니다. 그리고 이것을 어떻게 선택할지도 잠깐 생각해 보겠습니다.
앞선 글에서 \(\tau\)라는 모수치는 학교들 간 편차의 정도 (좀 더 일반적으로는 효과 크기의 변산성) 를 반영하는 값이라고 했었습니다. 이 값이 크면 학교들 간 편차가 크다, 작으면 편차가 작다는 의미였죠. 그런데 어느 베이지안 통계분석과 마찬가지로, 이 모수치에 대해서도 사전분포가 정해져야 후속 추론을 할 수 있습니다. 이 사전분포는 \(\tau\)의 크기와 그 불확실성에 대한 분석가의 사전 기대를 반영하는 것으로서, 신중하게 결정되어야 합니다. 앞선 글의 예제에서 등장한 코드를 잠깐 보면
schools <- bayesmeta(y=Rubin1981[,"effect"], sigma=Rubin1981[,"stderr"],
labels=Rubin1981[,"school"],
tau.prior=function(x){return(dhalfcauchy(x, scale=25))})
맨 끝 줄을 보면 tau.prior라는 argument에 다음과 같은 함수가 주어진 것을 볼 수 있습니다:
function(x){return(dhalfcauchy(x, scale=25))}
이것은 사전분포로 half cauchy distribution 이라는 것을 사용하겠다는 뜻입니다. half cauchy 분포는 코시분포 (자유도가 1인 t분포) 의 양의 부분만 취한 것인데, \(\tau\)는 표준편차라 음의 값을 가질 수 없기 때문에 오른쪽 절반만 잘라서 쓰는 것입니다. 특히 이 분포의 퍼진 정도를 결정하는 것은 scale 파라미터인데, 이 값이 클수록 사전분포의 퍼진 정도는 커집니다. 사전분포의 퍼진 정도가 클수록 \(\tau\)의 값이 클 수도 있다는 믿음을 반영하는 것이기 때문에, 우리는 scale 파라미터를 적절히 조절하여 분석가가 학교 간 편차에 대해 사전에 기대하는 정도를 분석에 반영할 수 있습니다.
여기서는 scale이 5, 10, 15인 세 경우를 예로 들어 사전분포를 시각화해 보겠습니다. 아래 그림에서 볼 수 있다시피, scale parameter의 값이 커질수록 \(\tau\)의 분포는 점점 납작해지고, 큰 값들에 대한 사전확률이 커지는 것을 알 수 있습니다. 이는 학교들 간 효과의 격차가 클 것이라는 사전 믿음을 반영합니다. 참고로 half cauchy 분포의 scale 파라미터 값은 곧 해당 분포의 중앙값인데, 이를 사전분포를 설정하는 데 참고할 수 있습니다. 이를테면 분석가가 \(\tau\)값이 10보다 클지, 작을지에 대한 믿음의 정도가 동일하다면 (대략 10 정도라고 생각한다면), 그 분석가는 \(\tau\)에 대한 자신의 사전 믿음을 scale=10으로 표현할 수 있는 것입니다.
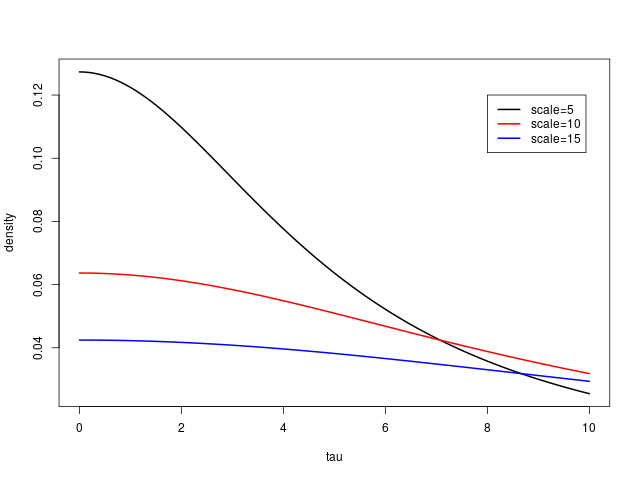
여기서 한 가지 예상할 수 있는 것은 \(\tau\)의 사전분포에 따라 각 학교의 효과의 참값 추정치들이 전체 평균으로 “당겨지는” 정도가 달라질 것이라는 점입니다. 즉 분석가가 scale 값을 작게 설정하면 이는 학교 간 차이가 작을 것이라는 믿음으로 이어져서, 추정치들이 전체 평균으로 강하게 당겨질 것이며, 크게 설정하면 반대로 추정치들이 shrink 되는 정도가 약할 것이라고 예측할 수 있습니다.
이제 이것이 실제로 일어나는지 확인해 보겠습니다. scale값을 5, 10, 15로 주고 각각의 메타분석 모형을 핏팅한 뒤,
library(bayesmeta)
data(Rubin1981)
schools_5 <- bayesmeta(y=Rubin1981[,"effect"], sigma=Rubin1981[,"stderr"],
labels=Rubin1981[,"school"],
tau.prior=function(x){return(dhalfcauchy(x, scale=5))})
schools_10 <- bayesmeta(y=Rubin1981[,"effect"], sigma=Rubin1981[,"stderr"],
labels=Rubin1981[,"school"],
tau.prior=function(x){return(dhalfcauchy(x, scale=10))})
schools_15 <- bayesmeta(y=Rubin1981[,"effect"], sigma=Rubin1981[,"stderr"],
labels=Rubin1981[,"school"],
tau.prior=function(x){return(dhalfcauchy(x, scale=15))})
각각에서 학교들의 효과 크기의 참값을 추출합니다:
> round(schools_5$theta,2)[5,]
A B C D E F G H
9.53 7.95 7.25 7.82 6.68 7.12 9.25 8.21
> round(schools_10$theta,2)[5,]
A B C D E F G H
10.32 7.97 6.92 7.78 6.18 6.78 9.83 8.37
> round(schools_15$theta,2)[5,]
A B C D E F G H
10.75 7.98 6.74 7.77 5.94 6.60 10.13 8.46
한 눈에 봐도 scale parameter의 크기가 커질수록 효과크기 추정치들이 점점 더 벌어지는 것을 볼 수 있습니다. 예를 들어 A학교의 경우, scale이 5였을 때는 9.53이었다가 scale이 15였을 때는 10.75로 다른 학교들과의 격차가 더 벌어졌습니다. 비슷한 현상을 다른 학교들에서도 관찰할 수 있습니다. 즉 사전분포가 퍼져 있을수록 shirinkage의 효과가 약해집니다.
이제 극단적인 경우를 생각해 봅시다. scale 값을 0에 아주 가깝게 주면 어떻게 될까요? 이는 학교 간 격차가 거의 없다는 사전믿음을 반영하기 때문에, 각 학교의 효과 추정치들은 전체 평균에 매우 강하게 당겨질 것입니다. 그러면 사전분포의 스케일 값을 0.01로 한 번 줘 봅시다:
> schools_smalltau <- bayesmeta(y=Rubin1981[,"effect"], sigma=Rubin1981[,"stderr"],
+ labels=Rubin1981[,"school"],
+ tau.prior=function(x){return(dhalfcauchy(x, scale=0.01))})
> round(schools_smalltau$theta,2)[5,]
A B C D E F G H
7.87 7.87 7.87 7.87 7.87 7.87 7.87 7.87
역시 짐작대로 되었습니다. 반대로 scale 값을 크게 줄수록 pooling의 효과는 점점 줄어들 것입니다.
지금까지 prior distribution이 분석 결과에 미치는 효과를 살펴보았습니다. 그 결과 prior의 설정이 후속 분석결과에 상당한 영향을 끼친다는 것을 알 수 있었습니다. 이렇게 prior를 변화시켜 가면서 결과의 변화 양상을 살펴보는 것은 Bayesian analysis에서 흔히 행해지는 것으로, good practice 의 조건으로 받아들여지고 있습니다.
마지막으로 조금만 더 첨언하면, 분석결과가 사전분포에 따라 달라진다는 게 안 좋은 것이냐? 여기 대해서는 사실 의견이 갈릴 수 있습니다. 누가 분석하든 똑같은 결과를 얻어야 한다고 생각하는 사람에게는 이게 단점일 것이고, 그렇지 않다고 생각하는 사람에게는 단점이 아닐 것입니다. 사실 후자의 부류 사람들에게는 사전정보가 있는 경우, 없는 경우에 비해 보다 더 informed analysis를 할 수 있어야 하는 것이 당연하게 받아들여질 것이기 때문에, 누가 분석하든 결과가 같다는 게 오히려 단점으로 비칠지도 모를겁니다. 중요한 것은 사전정보 자체가 정확해야 한다는 것입니다. 잘못된 사전정보의 투입은 분석을 망치는 지름길입니다. 따라서 prior의 생성 - prior eliictation 이라고 부릅니다 - 자체가 상당히 신중하게 이루어져야 한다는 것은 두말할 필요도 없습니다.