이번 포스트에서는 Nonparametric Bayesian 이 무엇인지 원리적인 부분에 대해 소개하고자 합니다.
Nonparametric Bayesian 은 이름에서 볼 수 있듯이 두 통계학 용어를 섞어 놓은 분야입니다. 요약하면 Bayesian 방식으로 nonparametric model 을 다루는 방법론입니다. 이 말을 자세히 이해하기 위해 먼저 이 블로그에서 다룰 모델(model) 의 범위와 불확실성(uncertainty) 을 측정하는 방법에 대해 자세히 이해해보도록 하겠습니다.
확률: 불확실성의 측도(measure of uncertainty)
통계학이나 머신러닝 이론을 다루는 대부분의 교과서는 첫 장부터 대게 확률론(probability theory) 을 먼저 배우게 됩니다. 확률은 불확실한 문제 상황에서 실현 가능한 경우의 수 들을 고려한 후, 전체 상황 중 어떤 사건이 발생할 가능성이 얼마나 되는지 척도(yardstick) 로 사용되는 개념입니다. 간단한 예로는 주사위 2개를 던졌을 때 합이 7 이 나올 확률은 얼마인지, 동전을 5번 던졌을 때 앞면이 연속해서 3번 나올 확률은 얼마인지 등의 문제를 풀 때, 우리는 가능한 경우들을 모두 생각해보고, 그 중 관심을 가지는 사건이 일어날 경우의 수를 세어봅니다.
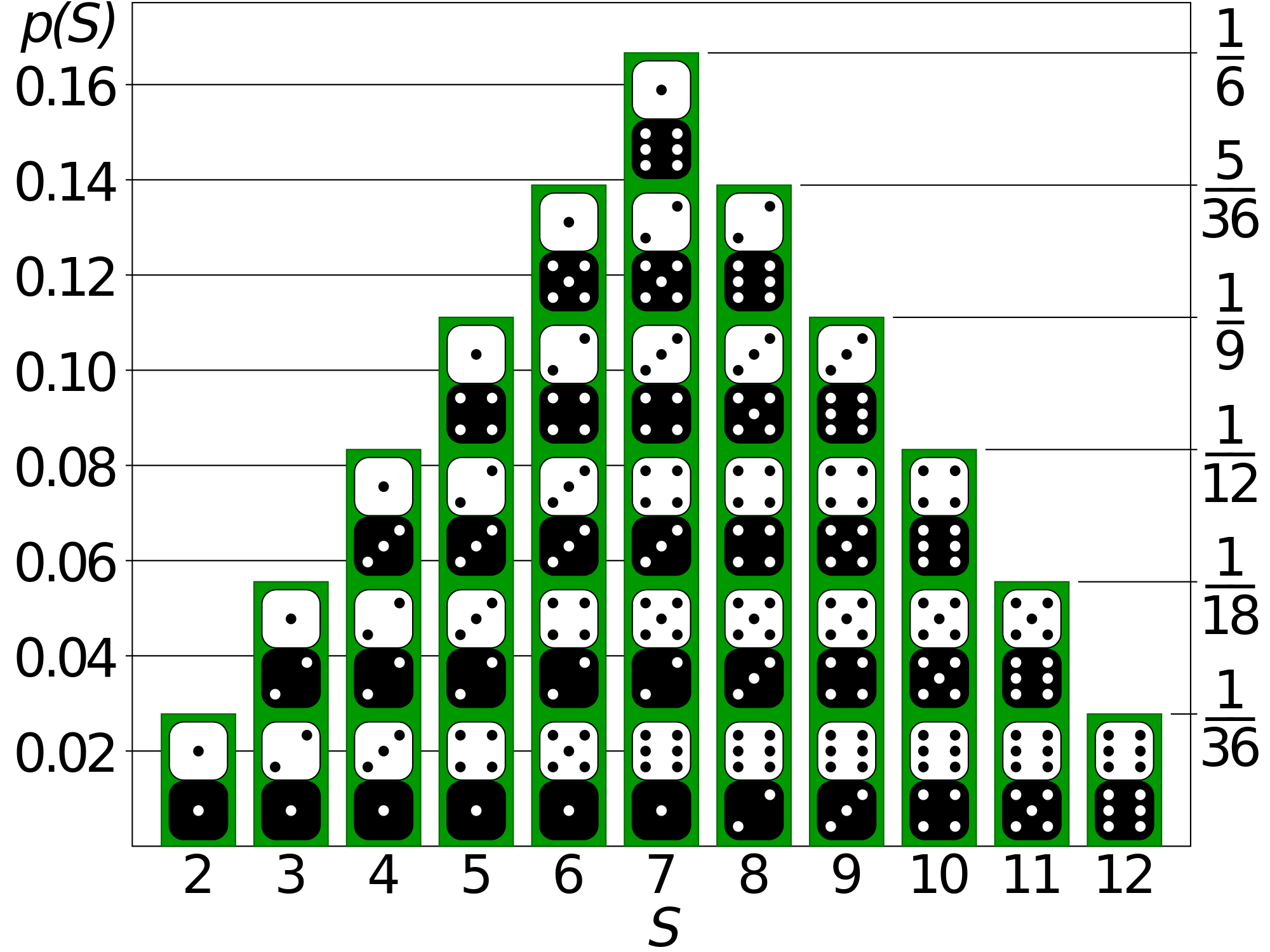 주사위 2개를 던졌을 때 가능한 합의 경우의 수와 확률분포, 출처: Math Stack Exchange
주사위 2개를 던졌을 때 가능한 합의 경우의 수와 확률분포, 출처: Math Stack Exchange
확률은 통계학이든 머신러닝에서든, 데이터를 측정하고 인과관계를 추론하고 미래를 예측하는 데 있어 현재까지 제일 유용한 수학적 개념입니다 [1]. 물론 이런 접근이 성공을 100% 보장하는 것은 아닙니다. 그러나 불확실성의 측도(measure of uncertainty) 라는 관점에서 확률은 우리가 기하학에서 배우는 길이, 넓이 같은 단어처럼 일상적인 용어가 되었고 현대 과학에서는 이미 떼놓을 수 없는 도구가 되었습니다. 뿐만 아니라 임상 실험, 주식 투자, 기업 의사결정 같은 문제에서도 가변적이고 다루기 까다로운 조건들을 변수로 고려해서 모델링을 할 때 확률을 사용하게 됩니다.
통계적 모델(statistical model)이란?
정량적인(quantitative) 분석이 요구되는 분야를 공부하다 보면 모델링의 종류가 어떻게 되는지, 어떤 모델링을 적용해야 하는지 고민하게 됩니다. 물리적 법칙 또는 governing dynamics 를 반영하여 모델을 결정론적인(deterministic) 형태로 기술할 수도 있지만 이는 굉장히 제한된(혹은 통제된) 환경에서 사용 가능한 것입니다. 반면 데이터를 기반으로 불확실성에 대한 적절한 가정 하에 통계적 모형(statistical model) 을 구축해서 적용할 수 있습니다.
통계적 모델이 무엇인지 이해하기 위해 예제를 하나 들어보겠습니다 (참조 출연: 오하이오의 낚시꾼).
Q: 오하이오에서 식당을 운영하는 낚시꾼 사장님은 서빙을 담당할 직원을 뽑으려고 한다. 한 직원이 시간대별로 응대할 수 있는 테이블의 숫자는 1개이고, 전체 테이블의 개수가 10개라고 하자. 직원을 몇 명을 뽑아야 할까?
위 문제를 언뜻 보면 전체 테이블 숫자와 같은 10명을 뽑아야 할듯 합니다. 그러나 실제 문제는 이렇게 간단하지 않습니다. 현실에선 낚시꾼 사장님은 다음과 같은 변수들을 같이 고려해서 의사결정을 내려야 하기 때문입니다.
- 직원에게 지불해야 하는 시급: \( P \)
- 테이블 \( i \) 에서 시간대 \( t \) 에 발생하는 수입: \( M(i,t) \)
- 시간대 \( t \) 별 식당을 방문하는 손님 그룹의 수: \( N(t) \)
여기서 \( P \) 는 고정된 비용이므로 결정적(deterministic) 변수 입니다 (낚시꾼 사장님은 마음이 착해서 시급을 최저임금보다 높게 준다고 가정합시다). 반면 2, 3번의 \( M(i,t), N(t)\) 는 확률적인(stochastic) 변수로 매시간마다 바뀌게 됩니다. 만약 직원을 전체 테이블 숫자만큼 채용하게 되면 테이블이 모두 꽉차는 \( (N(t) = 10) \) 피크 시간대에는 괜찮을지 몰라도 그렇지 않은 시간대는 \( (N(t) < 10) \) 손해를 볼 수 있습니다. 그러므로 낚시꾼 사장님은 이런 리스크를 고려해서 매출과 비용을 계산하여 적정 직원수를 채용해야 합니다. 낚시꾼 사장님이 하루에 \( T \) 시간동안 이 식당을 운영한다고 했을 때, 직원 \( X \) 명을 뽑았을 때 발생하는 매출 \( I \) 과 비용 \( C \) 을 계산해보면 아래와 같습니다 (기호 \( X \wedge N(t) \) 는 최소값 \( \min\{X, N(t)\} \) 을 뜻함):
여기서 \( \pi(X) \) 는 이윤에 해당합니다. 사장님이 이 식당을 손해 없이 운영하려면 매출이 비용보다 많은 \( \pi(X) > 0 \) 상태를 유지하는 \( X \) 를 찾아야합니다. 그러나 현실적으로 매출이 항상 비용보다 많기를 바라는 건 무리입니다. 왜냐하면 \( N(t) \) 와 \( M(i,t) \) 는 확률변수라서 최악의 경우일 때는 비용이 매출보다 큰 날도 발생할 수 있기 때문입니다. \( X \) 를 극단적으로 줄여서 운영하면 가능할수도 있지만 이윤이 하락하게 됩니다. 사장님은 부자가 되고 싶기 때문에 리스크를 좀 감당하려고 합니다. 그래서 경영 목표를 다음과 같이 바꿨습니다:
여기서 \( \alpha \) 는 매우 작은 값으로 (0.01 정도?) 낚시꾼 사장님이 감당할 리스크의 크기로 해석할 수 있습니다. 즉 \( (\star) \) 을 이용하면 손해가 발생할 확률이 \( \alpha \) 미만이 되는 범위 하에서 기대이윤(expected profit) \( \mathbb{E}[\pi(X)] \) 를 극대화하는 직원 수 \( X \) 를 찾는 문제가 됩니다. 고로 낚시꾼 사장님은 통계적으로 거의 손해를 보지 않는 범위 안에서 식당 운영이 가능해집니다.
분포를 알아내는 두 가지 방법: Parametric vs Nonparametric
그렇다면 남은 질문은, \( (\star) \) 에서 기대값과 확률은 어떻게 계산해야 할지입니다. 위의 예제를 다시 들여다보시면 결국 확률변수 \( M(i,t), N(t) \) 에 따른 매출 \( I \) 의 확률분포들을 알 수 있어야 \( (\star) \) 에 있는 기대값과 확률을 계산하는게 가능해집니다. 결론적으로 통계적 모델링은 적절한 가정 위에서 확률분포를 추정(inference) 하는 것이 목표입니다. 이는 머신러닝이든 통계학이든 공통적으로 추구하는 목표입니다.
 여러 종류의 확률분포, 출처: https://priorprobability.com
여러 종류의 확률분포, 출처: https://priorprobability.com
그런데 확률분포를 추론한다는 것은 어떤 의미일까요? 사실 유한한(finite) 개수의 데이터만 관찰해서 모집단의 정확한 분포를 알아낸다는 건 거의 불가능한 일입니다. 주어진 데이터를 통해 근사적(approximately)으로 확률분포를 추정할 수 밖에 없는데요, 이 때 어떤 전략을 취할지에 따라 모수적(parametric) 방법과 비모수적(nonparametric) 방법으로 나뉘게 됩니다. 두 방법의 차이를 (엄밀하지 않게) 직관적으로 서술한다면 아래와 같이 구분할 수 있습니다.
- Parametric: 데이터가 특정 확률분포를 따른다고 선험적으로(a priori) 가정한 후 그 분포를 결정하는 모수를 추정하는 방법. 추정해야 하는 모수의 개수가 고정(fixed) 되어 있고 절차적으로 변하지 않는다.
- Nonparametric: 특정 확률분포를 선험적으로 가정하지 않고 데이터에 따라 모델의 구조 및 모수의 개수가 유연하게(flexible) 바뀌는 방법 (주의: 모수가 없거나 부족하다는 뜻이 아니다)
두 방법론마다 나름의 장단점이 있기에 어떤 모델을 써야할지는 전적으로 연구자에게 달려있습니다. 물론 상황에 따라 더 적절한 방법론을 택해야 예측력이 높아지겠지요? 두 방법론의 차이를 조금 더 들여다 보겠습니다.
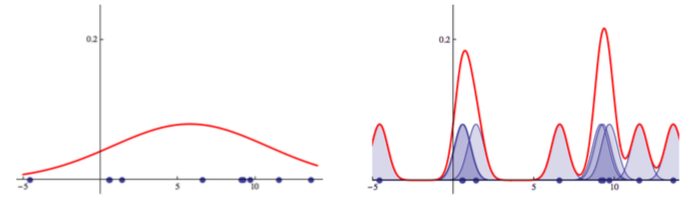 모수적(parametric) vs 비모수적(nonparametric) density estimation 방법 비교, 출처: P. Orbanz, 2014
모수적(parametric) vs 비모수적(nonparametric) density estimation 방법 비교, 출처: P. Orbanz, 2014
위 그림은 밀도 추정(density estimation)과 같은 예시에서 두 방법의 차이를 보여줍니다. 왼쪽 그림은 데이터가 정규분포 \( \mathcal{N}(\mu, \sigma^{2}) \) 를 따른다고 가정한 후 최대우도추정법(MLE, Maximum Likelihood Estimation)을 통해 평균 \( \mu \) 과 표준편차 \( \sigma \) 을 추정해서 찾은 확률밀도함수 입니다. 즉, 정규분포라는 특정 확률분포를 미리 가정한 후 모수에 해당하는 \( (\mu, \sigma) \) 를 추정하는 방법이며, 데이터의 숫자가 늘어나도 모수의 개수는 2개이므로 고정되어 있기에 모수적 방법에 속합니다. 반면 오른쪽 그림은 커널밀도추정(KDE, Kernel Density Estimation) 방법론으로서, 각 데이터 포인트 \( x_{i} \) 를 평균으로 가지는 정규분포 \( \mathcal{N}(x_{i}, \sigma^{2}) \) 를 정의한 후 그 확률밀도함수들의 산술평균 \( p_{n}(x) = \frac{1}{n}\sum_{i=1}^{n}p_{\mathcal{N}(x_{i},\sigma^{2})}(x) \) 로 확률분포를 추정합니다. 이 방법론에서 사용되는 모수의 개수는 데이터의 개수 \( n \) 에 비례하기 때문에 비모수적 방법에 해당합니다.
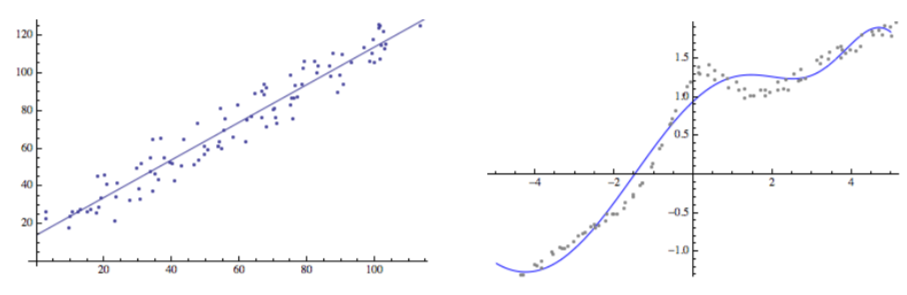 모수적(parametric) vs 비모수적(nonparametric) regression 방법 비교, 출처: P. Orbanz, 2014
모수적(parametric) vs 비모수적(nonparametric) regression 방법 비교, 출처: P. Orbanz, 2014
두 방법의 차이는 density estimation 뿐만 아니라 다른 task 인 regression 에서도 볼 수 있습니다. 왼쪽 그림은 주어진 데이터를 linear regression 으로 추정한 것입니다. Linear regression 은 주어진 데이터가 선형함수(linear function)를 따른다고 가정하고 regressor 를 \( \{f(x) = ax + b: a,b\in\mathbb{R} \} \) 라는 함수공간에서 찾으려고 합니다. 그러므로 추정해야 하는 모수는 기울기 \( a \) 과 \( y \)-절편 \( b \) 뿐 입니다. 따라서 데이터의 숫자가 늘어나도 추정해야 하는 모수의 개수는 변하지 않습니다. 반면에 오른쪽 그림은 주어진 데이터의 패턴이 nonlinear 합니다. 그러므로 regressor 를 매끄러운 함수(smooth function) 들의 집합, 가령 \( C^{2} \) 내에서 찾으려고 합니다. 일반적으로 이런 함수들을 알고리즘으로 찾아내려면 무한급수(series) 형태로 함수를 변형한 후 급수의 계수(coefficient)들을 추정해야 합니다. 그러므로 추정해야할 모수의 개수가 기본적으로 무한대가 되기 때문에 비모수적 방법으로 분류됩니다.
위에서 설명한 parametric 과 nonparametric 의 구분은 사실 덜 엄밀한 분류 방법입니다. 수학적으로 좀 더 명확하게 서술해보겠습니다. 데이터가 관찰 또는 수집되는 공간을 \( \mathcal{X} \) 라고 표기하겠습니다. 이 공간을 우리는 데이터 공간(data space) 또는 표본 공간(sample space)이라고 부릅니다. 수학 시간 때 배워온 자연수(\( \mathbb{N} \)), 정수(\( \mathbb{Z} \)), 실수(\( \mathbb{R},\mathbb{R}^{d} \)), 복소수(\( \mathbb{C} \)) 집합 등 우리가 흔히 사용하는 공간들이 \( \mathcal{X} \) 의 예 입니다 [2]. 그리고 이 공간 위에서 여러 확률분포(probability distribution)들을 정의할 수 있습니다. 가령 실수 공간 \( \mathbb{R} \) 이라면 정규분포(normal distribution) \( \mathcal{N}(\mu,\sigma^{2}) \) 나 지수분포(exponential distribution) \( \text{Exp}(\lambda) \) 등을 정의할 수 있겠지요. 이런 확률분포들을 모두 모아놓은 집합을 우리는 \( \mathbf{PM}(\mathcal{X}) \) 라고 표기하겠습니다. 당연하지만 이런 확률분포들은 셀 수 없을 정도로 무한히(uncountably) 많습니다 [2].
따라서 어떤 분포가 주어진 데이터를 모델링하기 적절한지 비교 분석을 하려면 모수공간(parameter space) 을 미리 결정해야 합니다. 이 모수공간을 \( \Phi \) 로 표기하고 그 원소 \( \theta\in\Phi \) 를 모수(parameter)라 하겠습니다. 그리고 이 \( \theta \) 를 통해 결정되는 확률분포 \( P_{\theta} \) 들의 집합을 \( M \) 으로 정의하겠습니다:
이 \( M \) 을 통계적 모델(statistical model) 혹은 줄여서 모델(model) 이라 부릅니다. 이 때 모수공간 \( \Phi \) 가 유한차원(finite-dimension) 이면 \( M \) 을 parametric model 이라 정의하고, \( \Phi \) 가 무한차원(infinite-dimension)이면 nonparametric model 이라 정의하게 됩니다. 위에서 설명한 두 방법론의 차이는 이와 같이 수학적으로 모수공간 \( \Phi \) 의 차원(dimension)의 개수에 따라 구별할 수 있습니다.
모델의 불확실성은 어떻게 추정하는가?
지금까지 확률분포를 추정하는 통계적 모델링의 방법론으로서 parametric 과 nonparametric 의 차이에 대해 알아보았습니다. 그렇다면 Nonparametric Bayesian 은 무엇일까요? 이를 설명하기 위해선 먼저 불확실성의 종류에 대해 알아볼 필요가 있습니다.
불확실성은 크게 아래 그림처럼 우연적인(aleatoric) 것과 인식적인(epistemic) 것으로 구분이 됩니다. 명확한 구별 방법은 아니지만 aleatoric 은 주로 데이터에 내재된 우연성에 의해 발생하는 불확실성이고, epistemic 은 잘못된 모델링 혹은 측정 방법에 기인한 불확실성입니다.
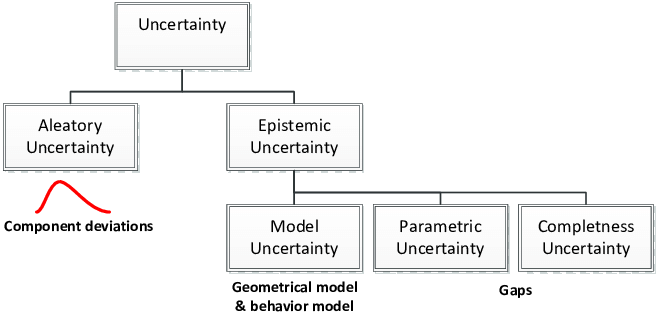 Taxonomy of Uncertainty, 출처: J. Y. Dantan et al., 2013
Taxonomy of Uncertainty, 출처: J. Y. Dantan et al., 2013
Bayesian 방법론은 흔히들 Bayes 정리 (Bayes’ theorem) 에 근간을 둔다고 합니다. 틀린 말은 아닙니다만, Bayes 정리를 사용한다고 모델이 Bayesian 이 된다는 뜻이 아닙니다. Bayesian 방법론의 기본적 원리는 모든 불확실성을 확률로 다루는 것 입니다. Bayesian 은 통계적 모델링에 사용되는 확률분포 \( P_{\theta} \) 를 결정하는 모수 \( \theta \) 는 본질적으로 unknown 이기 때문에 불확실성을 가지고 있다고 봅니다. 그러므로 Bayesian 방법론은 모델의 불확실성(model uncertainty)을 다루기 위해 모수 \( \theta \in \Phi \) 를 확률변수로 다룹니다. 즉 어떤 \( \Theta : \omega \mapsto \theta \) 를 도입해서 \( Q \) 라는 확률분포를 따른다고 전제합니다. 이 또다른 확률분포를 모델 \( M \) 의 사전분포(prior distribution) 라 합니다. 요컨데, Bayesian 은 다음과 같이 두 단계로 데이터가 생성된다고 가정합니다:
그리고 Bayes 정리를 통해 관찰된 데이터로 \( Q(\Theta \in \cdot | X_{1}=x_{1},\ldots, X_{n}=x_{n}) \) 라는 사후분포(posterior distribution) 를 유도할 수 있습니다. 요컨데, 이 사후분포를 통해서 모수 \( \Theta \) 의 불확실성을 고려하여 통계적 모델의 확률분포를 추정하는 것이 가능한 것입니다.
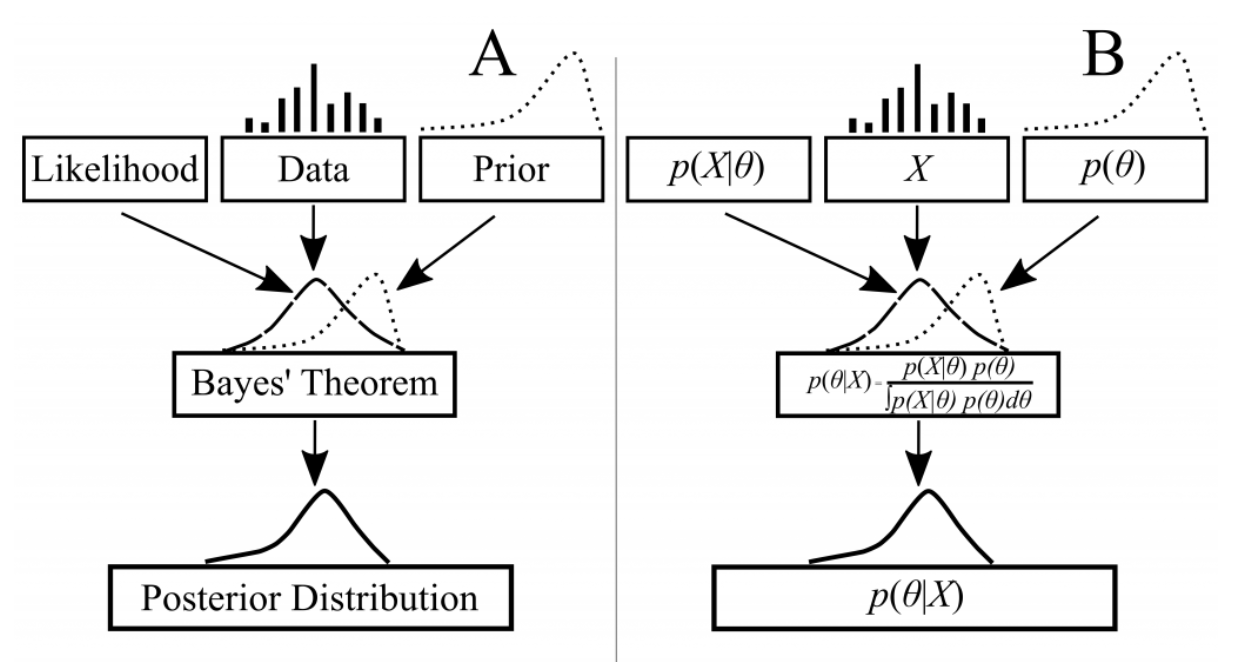 A Flow of Bayesian Inference, 출처: J. C. Doll & S. J. Jacquemin, 2018
A Flow of Bayesian Inference, 출처: J. C. Doll & S. J. Jacquemin, 2018
위에서 설명한 내용을 종합하면 Nonparametric Bayesian 은 모수공간 \( \Phi \) 가 무한차원 이고 \( \Phi \) 에 사전분포 \( Q \) 를 도입한 통계적 모델로서 최종적으로 사후분포를 계산해서 모수 \( \Theta \) 의 분포를 추정하는게 목적이라고 정리할 수 있습니다. 그렇다면 무한차원에 정의된 확률분포는 어떻게 상상해야 할까요? 확률론에서는 이 분포를 모수공간 \( \Phi \) 에 정의된 확률과정(stochastic process) 으로부터 유도가 가능합니다. Nonparametric Bayesian 강의에서 초반부부터 Dirichlet Process 를 포함하여 Indian Buffet Process 나 Gaussian Process 처럼 여러 확률과정들이 도입되는 이유가 이런 배경에서 기인했기 때문입니다.
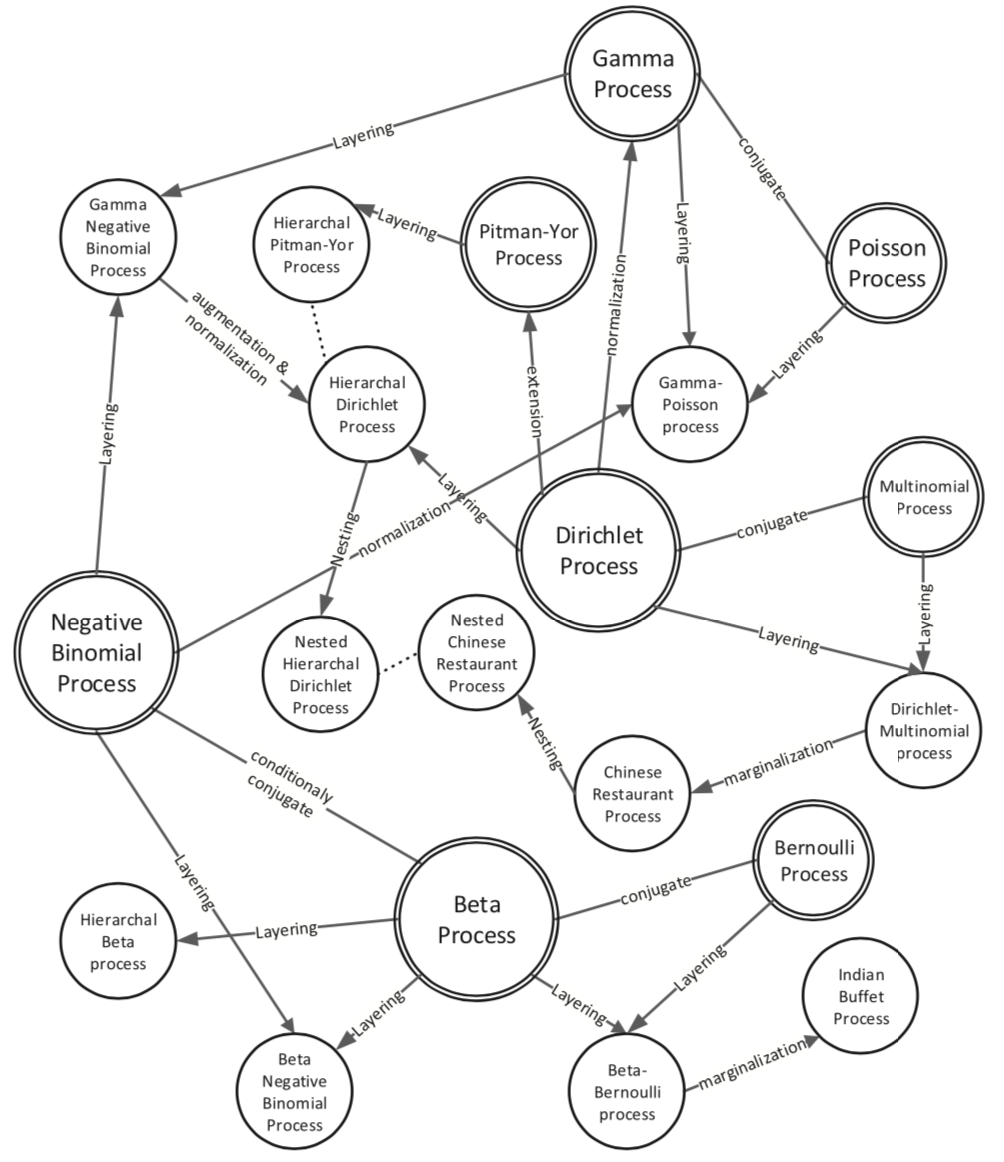 Nonparametric Bayesian 에서 사용되는 확률과정들의 관계들, 출처: J. Xuan et al., 2019
Nonparametric Bayesian 에서 사용되는 확률과정들의 관계들, 출처: J. Xuan et al., 2019
Why Nonparametric Bayesian?
모델이나 데이터에서 발생하는 불확실성의 정량화(quantification)는 머신러닝 연구분야에서 큰 주제 중 하나입니다. 의료나 금융처럼 불확실성이 의사결정에 큰 영향을 미치는 분야 외에도 로봇을 제어하거나 의료영상 데이터를 학습시킬 때 모델 예측이 틀릴 확률이나 확신(confidence)이 어느 정도 되는지 같이 요구됩니다. 이런 측면에서 nonparametric Bayesian 은 통계적 모델의 불확실성을 추정하는데 있어 유망한 방법론 중 하나입니다.
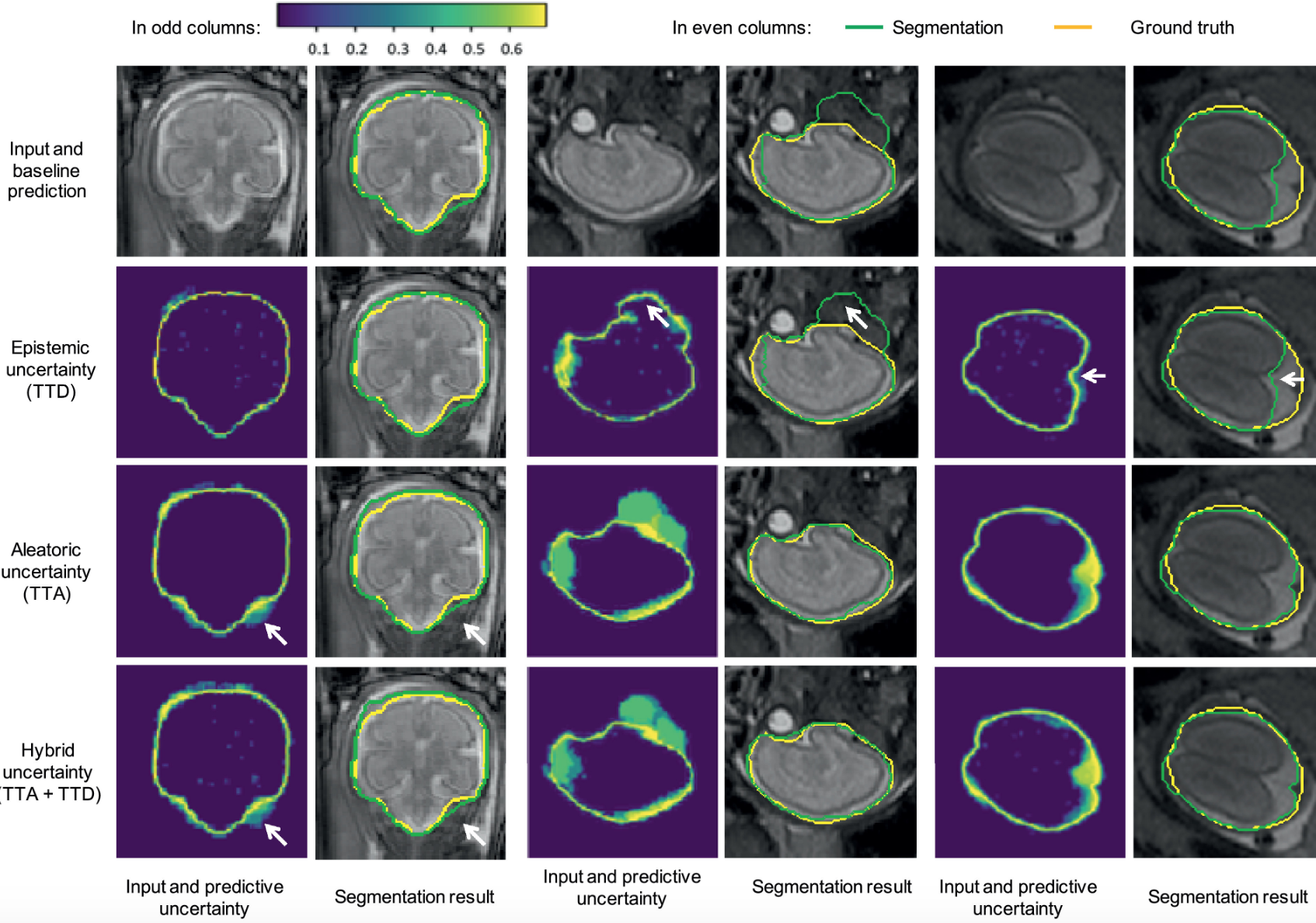 의료영상에서 Uncertainty Estimation, 출처: G. Wang et al., 2019
의료영상에서 Uncertainty Estimation, 출처: G. Wang et al., 2019
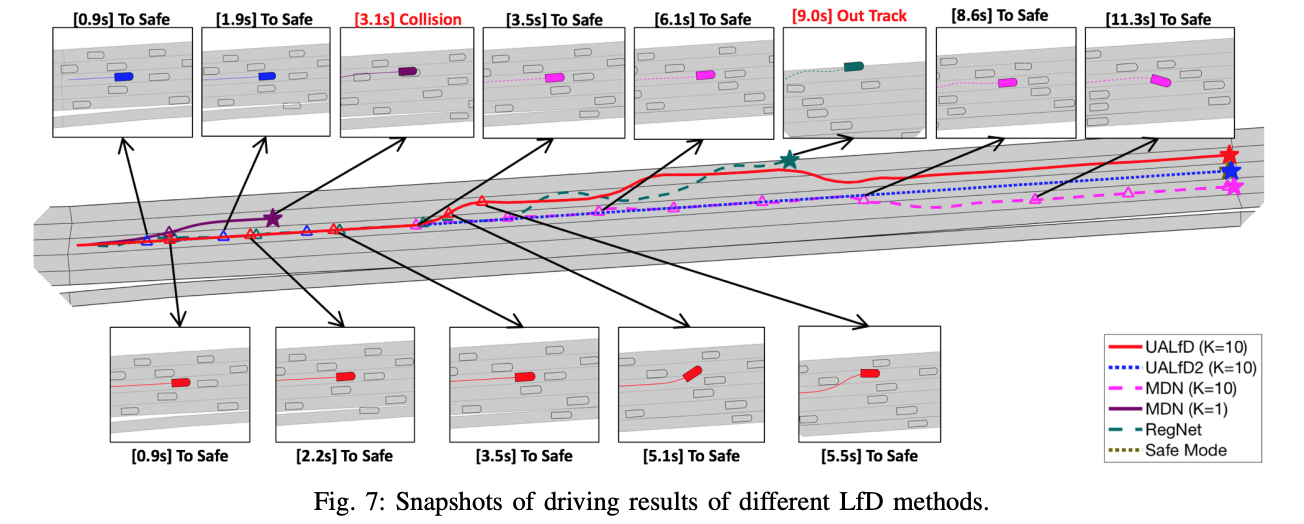 Uncertainty 를 고려한 Learning from Demonstration, 출처: S. Choi et al., 2018
Uncertainty 를 고려한 Learning from Demonstration, 출처: S. Choi et al., 2018
또한 hyperparameter optimization 나 NAS(Neural Architecture Search) 같은 AutoML 분야에서도 Bayesian 방법론을 사용하는 연구가 활발하게 진행되고 있습니다. AutoML 은 기본적으로 expensive-to-evaluate 상황에서 blackbox optimization 을 수행해야 합니다. 매번 오랜 시간동안 학습해야하는 모델의 최적선택을 해야하기 때문에 성능의 불확실성을 고려해서 유연하게(flexible) 최적화를 수행하는 nonparametric Bayesian 방법론이 유효한 선택이 되는 것입니다. 이 분야는 AutoML 에 관심을 가지는 각 연구소에서 현재 진행중인 주제이며 앞으로 많은 결과들이 쏟아질거라 기대됩니다.
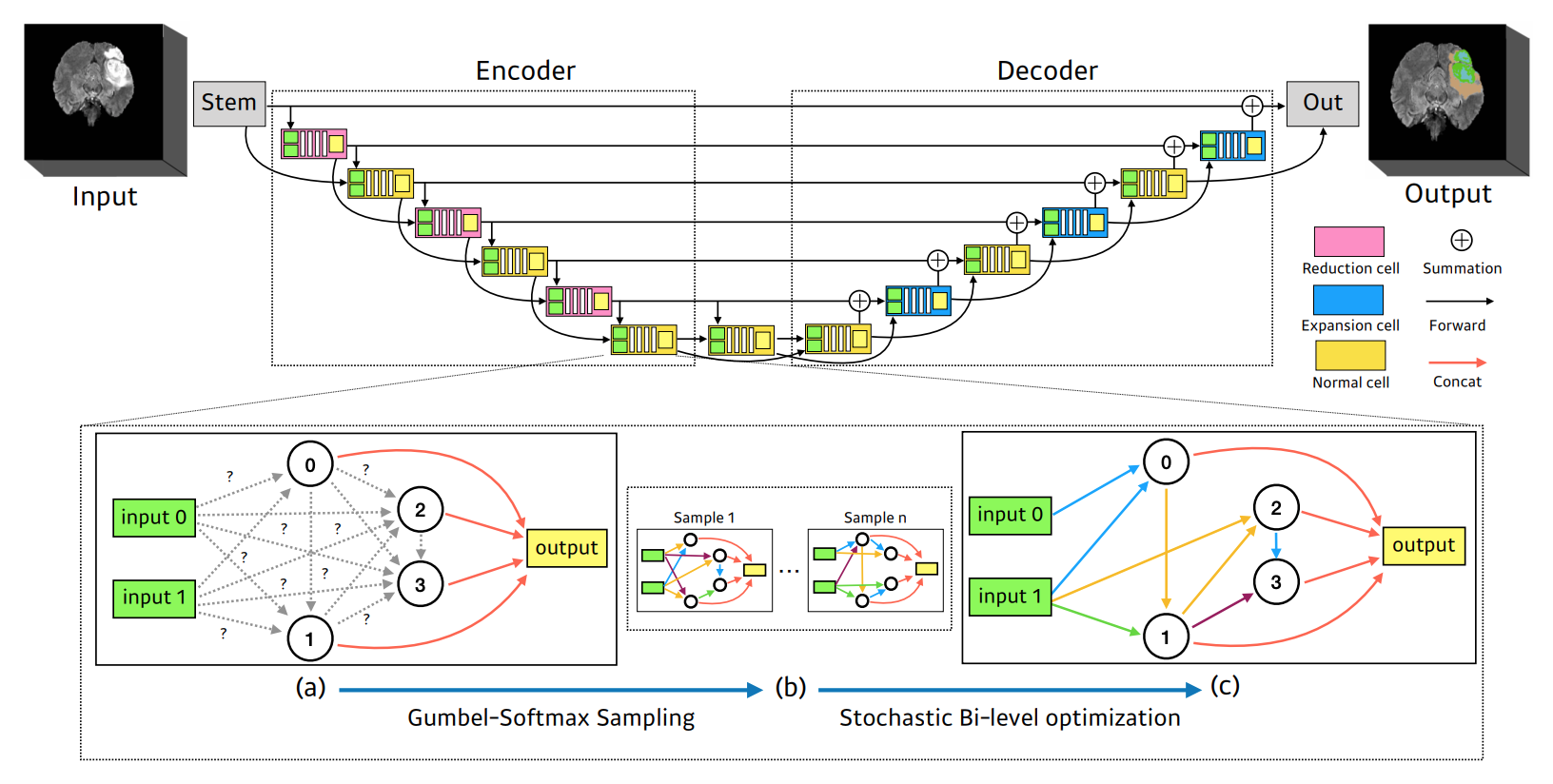 3D 의료영상에서 Gumbel-softmax 샘플링을 활용한 NAS, 출처: S. Kim et al., 2019
3D 의료영상에서 Gumbel-softmax 샘플링을 활용한 NAS, 출처: S. Kim et al., 2019
Comment
[1] 이런 해석에 대해 좀 더 궁금하신 분은 Bernardo 와 Smith 의 참고문헌(2000) 참조.
[2] 이론적으로는 Borel measure 를 정의할 수 있는 거리공간(metric space)이면 우리가 기본적으로 다룰 수 있는 공간입니다.
[3] 여기서 셀 수 없다(uncountable) 라는 의미는 수사적인 표현이 아니라 수학적인 용어입니다. 어떤 뜻인지 궁금하시다면 집합론(set theory) 교과서를 한 번 읽어보시길 추천합니다.
참고문헌
- Bayesian Theory, J.M. Bernardo, A.F.M. Smith (2000)
- Lecture Notes on Bayesian Nonparametrics, P. Orbanz, (2014)
- Bayesian Nonparametrics, J.K. Ghosh, R.V. Ramamoorthi, (2003)
- Bayesian Data Analysis, A. Gelman, J.B. Carlin, H.S. Stern, D.B. Dunson, A. Vehtari, D.B. Rubin, (2013)
-
Introduction to Bayesian Modeling and Inference for Fisheries Scientists, J. C. Doll, S. J. Jacquemin, (2018)
-
What Uncertainties Do We Need in Bayesian Deep Learning for Computer Vision?, A. Kendall & Y. Gal, (2017), NIPS
-
Uncertainty-Aware Learning from Demonstration Using Mixture Density Networks with Sampling-Free Variance Modeling, S. Choi, K. Lee, S. Lim, S. Oh, (2018), ICRA
-
Aleatoric uncertainty estimation with test-time augmentation for medical image segmentation with convolutional neural networks, G. Wang, W. Li, M. Aertsen, J. Deprest, S. Ourselin, T. Vercauteren, (2019)
-
A Survey on Bayesian Nonparametric Learning , J. Xuan, J. Lu, G. Zhang, (2019).
- Scalable Neural Architecture Search for 3D Medical Image Segmentation, S. Kim, I. Kim, S. Lim, W. Baek, C. Kim, H. Cho, B. Yoon, T. Kim, (2019), MICCAI.