(참고: 이 글의 예제들은 R의 결과값들을 중심으로 서술되어 있지만, Python의 경우에도 똑같이 적용됩니다.)
이 글은 앞의 Wald model에 대한 소개에서 이어집니다. 거기서 예고했던 대로 Bayesian estimation을 한 번 해 보도록 하겠습니다. Bayesian estimation을 위해서는 likelihood function과 prior만 있으면 됩니다. 그 뒤로는 MCMC 알고리즘만 “적절히” 짜 주면 샘플링은 알아서 잘 됩니다. 여기서 “적절히”라는 게 복잡한 모델의 경우에는 그리 쉽지 않다는 것이 함정입니다만, 지금 다룰 모델은 모수치가 3개짜리인, 그리 복잡하지 않은 모델이기 때문에 큰 문제는 없습니다.
참고로 이 예제에서는 단순화를 위해 prior를 따로 설정하지는 않겠습니다. 이는 사실 사전분포로 균등분포를 사용하는 것과 같습니다. 이는 “모수치의 어떤 값이든 똑같이 그럴듯하다” 또는 “모수치의 값에 대해 전혀 아는 바가 없다” 라는 분석가의 사전 믿음을 반영하는 것입니다. 하지만 사전분포를 포함시키는 것은 별로 어렵지 않습니다. 아래 코드에서 prior의 log값을 계산해서 likelihood에 더하는 부분만 추가하면 됩니다. 여기에 대해서는 더 깊게 이야기하지는 않겠습니다. [1]
여기서 사용할 MCMC 알고리즘은 Metropolis algorithm 입니다. 이 알고리즘은 모수치의 사후분포에 포함될 값의 후보 - proposal - 를 대칭적인 분포에서 제안합니다. 보통 proposal distribution은 uniform이나 normal을 많이 쓰는데, 여기서는 normal을 사용하겠습니다. 참고로 proposal distribution은 너무 넓게 퍼져있거나 너무 좁게 모여있어서는 안 됩니다. 전자의 경우에는 그럴듯하지 않은 값들이 propose 되기 때문에 굉장히 자주 reject된다는 단점이 있고, 후자의 경우에는 충분히 다양한 값들이 propose되지 않는다는 단점이 있습니다. 두 경우 모두 사후분포의 품질을 나쁘게 만들죠. 그래서 proposal distribution의 퍼진 정도 - 정규분포의 경우에는 분산(표준편차) - 는 “적절히” 설정되어야 하는데, 물론 여기서 “적절히”에 대한 절대적인 기준은 없습니다. 이리저리 try해 보면서 적절한 값을 찾는 것이죠. 그래서 MCMC 자체가 일종의 art와도 같다는 느낌을 받는지도 모르겠습니다. 방망이 깎던 노인급의 tuning이 때로는 필요합니다.
일단 예시로 사용할 자료를 생성하고, 최대가능도법으로 모델을 핏팅합니다:
#R
library(extraDistr)
set.seed(111)
n <- 100
t0 <- 0.35
data <- rwald(n, mu=0.5, lambda=0.5) + t0
mean(data)
sd(data)
minus_loglik <- function(t, parms){
z <- parms[1]
v <- parms[2]
t0 <- parms[3]
-sum(log(z*(2*pi*(t-t0)^3)^(-0.5)*exp(-(v*(t-t0)-z)^2/2/(t-t0))))
}
init <- c(.5, 1, 0.4)
fit <- optim(init, minus_loglik, t=data, control=list(maxit=10000, trace=1), hessian=T)
# Python
import numpy as np
import random
from scipy.stats import invgauss, norm, binom
from scipy.optimize import minimize
from numpy import log, exp, apply_along_axis, mean, median, std, quantile
from math import pi, isnan
random.seed(111)
n=100
t0=0.35
t = invgauss.rvs(mu=0.5, scale=1, size=n)+t0
def minus_loglik(parms):
z = parms[0]
v = parms[1]
t0 = parms[2]
return -sum(log(z*(2*pi*(t-t0)**3)**(-0.5)*exp(-(v*(t-t0)-z)**2/2/(t-t0))))
init = [.5, 1.2, .3]
fit = minimize(minus_loglik, init, method="nelder-mead")
최대가능도 추정치는 다음과 같습니다:
#R
fit$par
[1] 0.5689837 1.3074652 0.4012044
# Python
print(fit.x)
[1.10135411 2.22615627 0.32785858]
이제 베이지안 추정을 위해 MCMC sampler를 짜 봅시다. 먼저 log-likelihood를 계산해 주는 함수를 짜고,
# R
loglik <- function(t, parms){
z <- parms[1]
v <- parms[2]
t0 <- parms[3]
sum(log(z*(2*pi*(t-t0)^3)^(-0.5)*exp(-(v*(t-t0)-z)^2/2/(t-t0))))
}
# Python
def loglik(parms):
z = parms[0]
v = parms[1]
t0 = parms[2]
return sum(log(z*(2*pi*(t-t0)**3)**(-0.5)*exp(-(v*(t-t0)-z)**2/2/(t-t0))))
그 다음으로 Metropolis 샘플러를 작성합니다:
# R
metropolis <- function(t, parms, proposal_sd){
# propose from normal
proposal <- parms + rnorm(length(parms), 0, proposal_sd)
# compute ratio
num <- loglik(t, proposal)
den <- loglik(t, parms)
r <- exp(num-den)
if(is.nan(r)) return(parms)
else {
if(r > 1) return(proposal)
else {
if(rbinom(1, 1, r) == 1) return(proposal)
else return(parms)
}
}
}
# Python
def metropolis(t, parms, proposal_sd):
# propose from normal
proposal = parms + norm.rvs(loc=0, scale=proposal_sd, size=len(parms))
# compute ratio
num = loglik(proposal)
den = loglik(parms)
r = exp(num-den)
if(isnan(r)):
return(parms)
else:
if(r > 1):
return(proposal)
else:
coin = binom.rvs(1, r, size=1)
if(coin == 1):
return(proposal)
else:
return(parms)
이 함수는 세 개의 입력값을 받는데, t는 데이터, parms는 “현재” 모수치들의 값, proposal_sd는 proposal distribution의 표준편차를 의미합니다. 입력값을 받은 후, 이 함수는 현 모수치들의 값에 0을 중심으로 한 정규분포에서 표집한 값들을 더해 proposal을 만든 후, 그것과 현 모수치 값 하에서 각각 계산된 log-likelihood 값들의 비율을 계산합니다. 이것이 1을 넘으면 그냥 proposal을 accept 하고, 그렇지 않으면 likelihood 값들의 비율을 성공 확률로 “동전”을 던져, “앞면”이 나오면 proposal을 수락하고, 아니면 기각한 후 현 모수치 값을 다시 수락합니다. 이 작업을 반복하여 샘플링을 하는 것이 Metropolis 알고리즘의 핵심입니다.
이제 실제로 샘플링을 해 보겠습니다.
# R
# sample from posterior
proposal_sd <- 0.01
n_mcmc <- 10000
accept <- 0
post <- matrix(nrow=n_mcmc, ncol=3)
# use ML estimates as initial values
post[1,] <- fit$par
for(i in 2:(n_mcmc)){
post[i,] <- metropolis(data, post[i-1,], proposal_sd)
if(sum(post[i,] == post[i-1,]) < 3) accept <- accept + 1
}
# Python
# sample from posterior
proposal_sd = 0.01
n_mcmc = 10000
accept = 0
post = np.zeros([n_mcmc, 3])
# use ML estimates as initial values
post[0,:] = fit.x
for i in range(n_mcmc-1):
post[i+1,:] = metropolis(data, post[i,:], proposal_sd)
if sum(post[i,:] == post[i-1,:]) < 3:
accept += 1
Proposal distribution의 표준편차는 0.01로 설정하고, 샘플은 총 10,000개를 추출합니다. accept라는 변수는 proposal이 수락된 횟수를 저장하는 변수로, 이것을 sampling 횟수로 나누면 proposal이 수락된 비율, 즉 acceptance rate 라는 것을 얻습니다. acceptance rate는 충분히 높아야 샘플의 질을 보장할 수 있습니다. 그렇지 않으면 특정 값들이 반복적으로 저장된 횟수가 너무 높아지니까요.
이제 모아진 샘플에서 앞의 절반을 버리고 (burn-in이라고 합니다), 나머지를 시각화합니다. 꼭 절반이나 버릴 필요는 없지만, 안전하게 많이 버렸습니다. 시각화는 시계열 플롯으로 보면 됩니다. 이를 Traceplot이라고 부릅니다:
# R
# throw away pre-burn-in samples
post_burnin <- post[(n_mcmc/2+1):n_mcmc,]
# Traceplots
par(mfrow=c(3,1))
for(i in 1:3){
plot.ts(post_burnin[,i])
}
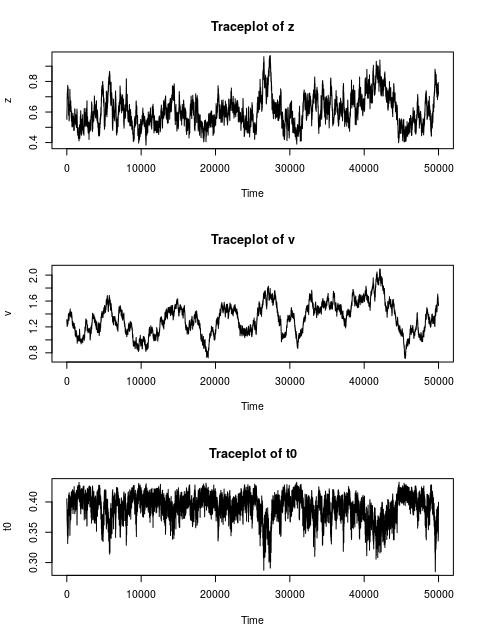
# Python
# throw away pre-burn-in samples
post_burnin = post[int(n_mcmc/2):,]
import matplotlib.pyplot as plt
plt.plot(range(int(n_mcmc/2)), post_burnin[:,0])
plt.plot(range(int(n_mcmc/2)), post_burnin[:,1])
plt.plot(range(int(n_mcmc/2)), post_burnin[:,2])
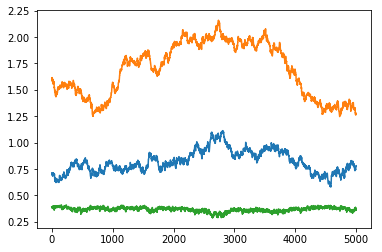
체인들을 보면 특정 값을 중심으로 계속 오르락 내리락 하는 것을 볼 수 있는데, 이것은 MCMC chain들이 목표로 하는 사후분포로부터 샘플이 잘 되었다는 것의 한 증거입니다. 이를 “수렴했다” convergence 라고 이야기합니다. MCMC 체인들의 수렴은 사후분포에 대한 올바른 추론을 위한 중요한 조건입니다.
이제 사후분포의 평균과 중앙값을 앞에서 얻은 maximum likelihood 추정치와 비교해 보도록 하겠습니다:
# R
# compute posterior means and medians for model parameters
postmean <- colMeans(post_burnin)
postmedian <- apply(post_burnin, 2, median)
# estimates
ests <- cbind(postmean, postmedian, fit$par)
rownames(ests) <- c("z","v","t0")
colnames(ests) <- c("postmean","postmedian","ML")
round(ests, 3)
postmean postmedian ML
z 0.605 0.594 0.569
v 1.331 1.338 1.307
t0 0.392 0.396 0.401
# Python
# compute posterior means and medians for model parameters
postmean = apply_along_axis(mean, 0, post_burnin)
postmedian = apply_along_axis(median, 0, post_burnin)
# estimates
ests = [postmean, postmedian, fit.x]
np.round(ests, 3)
[[1.001 2.039 0.341]
[0.995 2.025 0.344]
[1.101 2.226 0.328]]
각 행(파이썬 예제에서는 열)은 z, v, t0에 해당됩니다. 그리고 첫 번째 열[행]은 사후분포로부터 얻은 평균, 두 번째 열[행]은 사후분포의 중앙값들, 그리고 마지막 열[행]이 ML 추정치입니다. 추정치들은 대체로 비슷한 것 같습니다.
이제 각 모수치들의 사후 표준편차를 계산하겠습니다. 이 값들은 추정치에 대한 업데이트된 불확실성을 나타냅니다:
# R
apply(post_burnin, 2, sd)
[1] 0.09973272 0.24178686 0.02050735
# Python
apply_along_axis(std, 0, post_burnin)
[0.12995002 0.14920032 0.02983849]
그리고 각 모수치에 대한 95% 구간추정치 (신용구간) 들도 만들 수 있겠습니다:
# R
> quantile(post_burnin[,1], c(.025, .975))
2.5% 97.5%
0.4475114 0.8348677
> quantile(post_burnin[,2], c(.025, .975))
2.5% 97.5%
0.8897098 1.8050179
> quantile(post_burnin[,3], c(.025, .975))
2.5% 97.5%
0.3431149 0.4215478
# Python
print(quantile(post_burnin[:,0], [.025, .975]))
[0.78002601 1.25728771]
print(quantile(post_burnin[:,1], [.025, .975]))
[1.78842439 2.35306908]
print(quantile(post_burnin[:,2], [.025, .975]))
[0.27290391 0.38854148]
z의 신용구간은 [.45, .83], v는 [0.89, 1.81], t0는 [0.34, 0.42] 가량인 것을 볼 수 있습니다. 마지막으로 acceptance rate를 확인하면 63% 가량인 것을 확인할 수 있습니다. 이 정도는 괜찮은 값이라고 할 수 있습니다. 일반적으로 권장되는 값은 65%입니다:
# R
accept/(n_mcmc-1)
[1] 0.6315263
# Python
print(accept/(n_mcmc-1))
0.7682768276827683
참고로 앞에서 proposal distribution들의 sd가 너무 작거나 크면 샘플링이 잘 안 된다고 했었습니다. 이를 확인하기 위해 sd를 0.00001 또는 1로 설정하고 다시 샘플링을 한 뒤 acceptance rate를 확인해 보면 전자에서는 1에 가깝고 후자에서는 0.0001도 안 됩니다. 즉 전자에서는 너무 “안전한” proposal들만 제안한 나머지 충분히 다양한 값들을 탐색해 보지 않은 것이고, 후자에서는 너무 말도 안 되는 값들만 제안된 나머지 대부분이 reject된 것입니다. 따라서 proposal distribution의 표준편차는 “적절히” 설정되어야 합니다. (김대기급…이라고 하면…모르시는 분들이 많겠죠.)
지금까지 Wald 모형을 가지고 MCMC 샘플링과 베이지안 추론을 해 보았습니다. 이 예제에서는 prior를 따로 설정하지 않았지만, 이를 더하는 것은 크게 어렵지 않습니다. log-likelihood에 log-prior의 값만 더해주면 됩니다. 이와 같은 방법을 다른 모델들에도 적용할 수 있습니다. 이를테면 반응시간의 다른 모형들로 ex-Gaussian model, Linear Ballistic Accumulator (LBA) 와 Drift diffusion model (DDM) 이라는 것들이 있는데, 이것들도 MCMC를 활용한 Bayesian estimation이 가능합니다. R의 경우 이를 위한 함수들을 제공해 주는 rtdists 패키지를 사용하면 됩니다. 단, 한 가지 주의할 사항이 있습니다. 이런 모델들은 흔히 추정치들 간 상관이 높습니다. 이를테면 큰 z의 값에 대해서는 큰 v의 값이, 작은 z의 값에 대해서는 작은 v의 값이 샘플링되는 경향이 있다는 것입니다. 이런 모델을 sloppy model이라고 부르는데, 이런 상황에서는 Metropolis algorithm 같은 간단한 기법은 - 특히 hierarchical model 에서는 - 낮은 acceptance rate로 인해 잘 작동하지 않는 경우가 많습니다. 이런 상황에서는 좀 더 고급 샘플링 기법을 사용해야 합니다. 그 중 비교적 구현하기 쉬운 것으로는 Differential Evolution MCMC (DE-MCMC) 라는 기법이 있는데, 이는 참고문헌 [2]에 잘 서술되어 있습니다.
[1] 사실 실험에서 관찰되는 RT의 분포나 추정된 non-decision time의 값은 어느 정도 알려져 있기 때문에, 이를 반영하는 informative prior를 사용하는 게 바람직할 수도 있습니다.