Likelihood-free Bayesian inference (2): 이항분포 예제

예고했던 대로 이 글에서는 가장 간단한 ABC rejection sampling을 구현해 보도록 하겠습니다. 다음 확률모형을 생각해 봅시다:

$Y \sim \mbox{Binomial}(10, p) ... (1)$

$Y$는 시행횟수가 10, 성공률이 $p$인 이항분포를 따릅니다. 이제 여기서 $Y=6$이라는 데이터를 얻었다고 가정하고, 이것을 가지고$p$에 대한 업데이팅을 해 봅시다. 여기서$p$에 대한 사전분포는 균등분포, 즉 $\mbox{Beta}(1,1)$로 가정합니다. 사실 이렇게 사전분포가 베타분포, 확률모형이 이항분포인 경우 [1] 사후분포를 얻는 것은 매우 쉽습니다. 예전에 한 차례 이야기했던 대로, 베타사전분포의 두 모수치에 각각 성공, 실패 횟수를 더해주기만 하면 됩니다. 그러면 다음을 얻습니다:

$p|y \sim \mbox{Beta}(1+6,1+4)... (2)$

이 이론적 사후분포의 기댓값은 $7/(7+5)=0.583$, 표준편차는 $\sqrt{\frac{7(5)}{(7+5)^2(7+5+1)}}=0.1367$ 입니다. 자세한 공식은 위키 항목을 참조하시기 바랍니다.

이제 ABC rejection sampling으로 이 결과를 재현할 수 있는지 보겠습니다. 앞 글에서 말했던 것처럼 이 알고리즘은 다음의 세 스텝으로 이루어져 있습니다:

사전분포에서 모수치 제안
제안된 모수치를 이용해 자료 생성
생성된 자료가 실제 획득된 자료와 비슷한지 판단 후 제안된 모수치 accept 할지말지 결정, 만약 reject되었다면 다시 1부터 시작

이것을 위 사례에 적용하면 다음과 같습니다:

$\mbox{Beta}(1,1)$ 또는 $\mbox{Uniform}(0,1)$ 에서 $p$를 제안 (두 분포는 같은 분포입니다).
제안된 $p$를 이용하여 $\mbox{Binomial}(10, p)$로부터 자료 무선추출.
추출된 값이 실제로 관측된 자료 $(Y=6)$ 와 “비슷하면” 제안된 $p$를 수락, 아니면 1로 리턴. 수락되는 값이 나올 때까지 반복.

이 1-3이 사후분포 샘플 한 개를 추출하는 한 바퀴입니다. 그리고 이것을 원하는 사후분포 샘플 크기가 채워질 때까지 계속 반복하면 됩니다. 여기서 생성된 자료와 실 자료가 비슷한지 판단하는 기준이 필요한데, 이 예제에서는 그냥 간단하게 똑같은 자료가 생성되어야만 accept 한다고 가정하겠습니다. 그러니까 2. 에서 $Y=6$이 생성되는 경우에만 그것을 accept 하여 사후분포에 넣겠다는 뜻입니다. 이 기준은 꽤 빡빡하지만, 아주 좋은 사후분포를 만들어 줍니다.

R 및 파이썬 코드는 아래와 같습니다. 사실 몇 줄 되지도 않습니다:

# R

sampler <- function(n, y){
  
  dif <- 1
  sim <- n+1
  
  while(sim != y){
    
    p <- runif(1)
    sim <- rbinom(1, n, p)

  }
  
  p
  
}

n <- 10
y <- 6
n_sample <- 100000
post <- vector(length=n_sample)

for(i in 1:n_sample) post[i] <- sampler(n, y)

# Python

import numpy as np
from numpy.random import binomial, uniform
import matplotlib.pyplot as plt
%matplotlib inline

n = 10
y = 6

def sampler(n,y):
    
    sim = n+1
    
    while sim != y:
        
        p = uniform(0, 1, 1)
        sim = binomial(n, p, 1)
        
    return p

n_sample = 1000
post = []

for i in range(n_sample):
    post.extend(sampler(n,y))
    
print(np.mean(post))
print(np.std(post))

plt.hist(post, 20,
         density=True,
         histtype='bar',
         alpha=0.5)

plt.show()

각각의 코드에서 sampler라는 이름의 함수를 읽어보시면 제가 앞에서 말한 것을 그대로 구현했음을 알 수 있습니다. 이를 이용하여 100,000개의 샘플을 추출하여 post라는 변수에 저장했습니다. 아래 그림은 R에서 얻은 post의 히스토그램과 true posterior인 $\mbox{Beta}(7,5)$를 함께 그린 것인데, 거의 일치한다는 것을 알 수 있습니다.

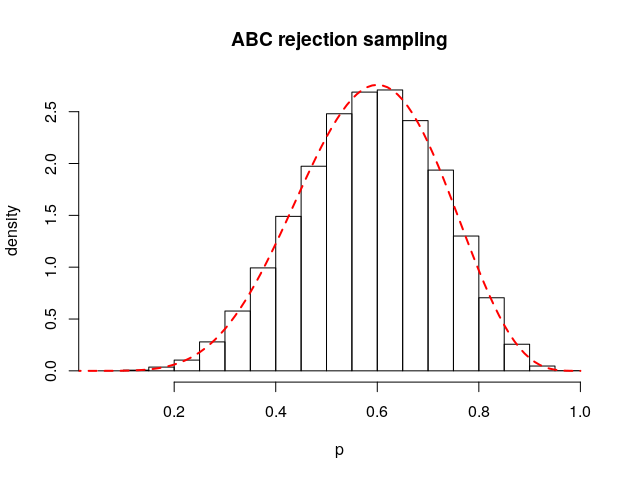
샘플의 평균과 분산도 계산해 보면 다음과 같습니다:

> mean(post)

[1] 0.5835859

> sd(post)

[1] 0.1367117

두 숫자 모두 아까 이야기했던 이론적 값인 0.583과 0.1367과 거의 일치한다는 것을 알 수 있습니다.

지금까지 간단한 ABC rejection sampling의 사례를 보여드렸습니다. 사실 이 사례는 ABC rejection sampling이 매우 잘 작동한 사례인데, 여기에는 하나 숨어있는 이유가 있습니다. 그것은 자료들 간의 ‘비슷함’을 평가하는 데 사용된 통계량 - $y$ 자체 - 이 모수치에 대한 충분통계량 sufficient statistic 이었다는 것입니다. 통계학에서 충분통계량이라는 개념은 매우 중요한 개념인데, 어떤 통계량이 “충분”하다는 것은 모수치에 대해 자료가 제공하는 모든 정보를 해당 통계량이 담고 있다는 것입니다. 그러니까 여기서 $Y$는 $p$에 대한 모든 정보를 담고 있는 충분통계량인 것입니다. (놀랍지 않게 정규분포의 경우, 모평균에 대한 충분통계량은 표본평균이며 모분산에 대한 충분통계량은 표본분산입니다.) 이런 값이 rejection을 결정하는 단계에서 데이터들 간의 비슷함을 평가하는 데 사용되면, 모수치에 대한 가용한 모든 정보가 사용되기 때문에 ABC 알고리즘은 굉장히 잘 작동합니다. 이 예제의 경우 거의 true posterior에 가까운 사후분포를 얻을 수 있었죠. 하지만 일반적으로 ABC가 적용되는 모형들은 꽤 복잡하고 수학적 표현이 알려져 있지 않기 때문에 충분통계량이 무엇인지 알기 힘든 경우가 대부분입니다. 그래서 어쩔 수 없이 연구자는 모수치에 대해 가장 많은 정보를 담고 있을 것으로 추측되는 통계량을 선택하여 자료들 간의 거리를 계산할 수밖에 없는데, 이것을 선택하는 것이 ABC에서 상당히 중요한 문제입니다.

이 글에서는 이산형 분포를 다루었는데, 다음 글에서는 연속형 분포인 정규분포를 가지고 ABC rejection sampling을 해 보도록 하겠습니다. 이 경우에는 생성된 자료가 원 자료와 완전히 똑같을 확률이 0이기 때문에 accept/reject를 판단할 때 좀 다른 전략이 필요합니다. 자세한 것은 다음 글에서 이야기하겠습니다.

[1] 이를 Beta-Binomial model이라고 부릅니다. 여기서 Beta 사전분포는 Binomial model에 대한 켤레사전분포 conjugate prior인데, 사전분포가 켤레사전분포인 경우에는 따로 샘플링 없이 바로 사후분포를 닫힌 형태로 얻을 수 있기 때문에 매우 간편합니다. 켤레사전분포는 MCMC가 등장하기 이전에 특히 베이지안 추론에서 널리 사용되었습니다.

Bayesian Statistics